Cartografia e navigazione cartografica
La cartografia e le carte di navigazione sono gli elementi indispensabili per la navigazione marittima e aerea, permettendo di determinare la posizione di un punto sulla superficie terrestre attraverso l'uso di mappe e strumenti di misurazione.
Il problema della posizione
Sin dagli albori della Storia c'era l'esigenza di capire dove ci si trovava in base alle caratteristiche del territorio circostante e quali erano le direzioni da dover prendere (e le distanze associate) per raggiungere altri centri abitati o punti di rilievo commerciale.
Viaggiando su terra e soprattutto in mare era fondamentale conoscere e annotare su carta i pericoli che si incontravano e le varie distanze di viaggio: per questo motivo i primi viaggiatori iniziarono a compilare le primissime carte geografiche, come la Tabula Peutingeriana.
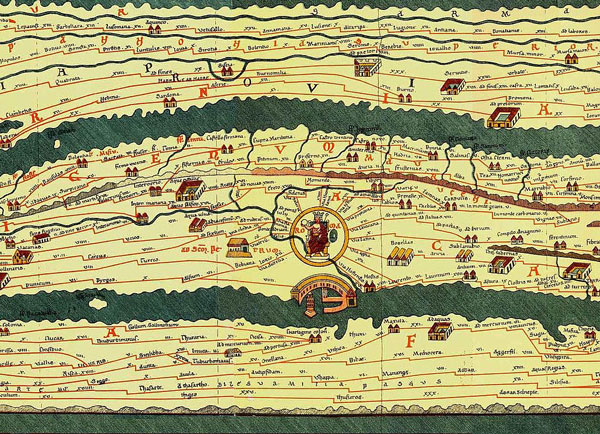
Tabula Peutingeriana con al centro Roma
Conradi Millieri - Ulrich Harsch Bibliotheca Augustana, Pubblico dominio
La necessità della precisione
Ad un certo punto il Mondo conosciuto ha iniziato ad espandersi sempre più velocemente e la sola indicazione della lunghezza o "Longitudo" di un percorso da un punto all'altro non è stata più sufficiente: bisognava sviluppare un metodo matematico per indicare con precisione la propria posizione rispetto ad alcuni punti di riferimento notevoli.
Finché si parlava di distanze e lunghezze, il percorso poteva tranquillamente essere rappresentato come una retta su cui piazzare delle "pietre miliari" per indicare la distanza da un certo punto.
Quando, invece, è diventato necessario indicare le posizioni di luoghi di interesse nello spazio e - più specificatamente - su di una carta geografica, il solo asse delle distanze non bastava più: bisognava aggiungere un secondo asse, quello della larghezza o "Latitudo", perpendicolare a quello della "Longitudo".
Il metodo del piano e delle coordinate cartesiane, sviluppato dal matematico e filosofo francese René Descartes (Cartesio), portò a una grande rivoluzione nella cartografia. Per indicare una posizione ben precisa non bisognava più indicare "cammina lungo il fiume per 2 giorni e poi sali verso i monti per mezza giornata" ma bastavano due semplici indicazioni: le distanze rispetto a un asse orizzontale e a un asse verticale. Questi assi perpendicolari rappresentano gli assi "zero" di riferimento del piano cartesiano.
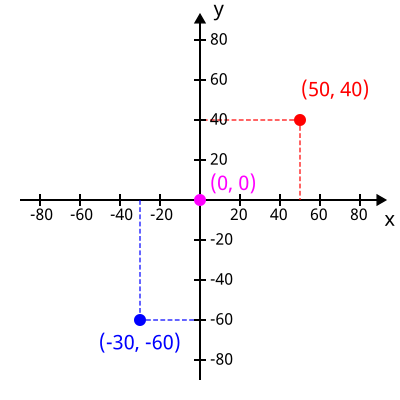
Latitudine e Longitudine: il sistema di coordinate geografiche
Per utilizzare le coordinate cartesiane in un sistema sferico, bisogna innanzitutto creare un reticolo di "riferimento". Per questo motivo sono stati introdotti i meridiani (circoli massimi che passano per i poli) e i paralleli (il cui unico circolo massimo è l'Equatore). In sostanza i meridiani dividono la Terra in spicchi mentre i paralleli la "tagliano" in fette orizzontali.
L'Equatore divide la Terra in due emisferi: un emisfero Nord (detto anche "boreale") e un emisfero Sud (detto anche "australe").
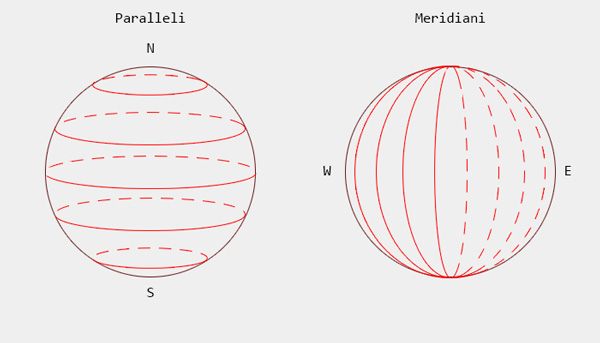
I meridiani sono tutti identici mentre i paralleli si accorciano man mano che si va verso i poli. Questo è il motivo fondamentale per cui sulle carte nautiche per misurare le distanze si prendono a riferimento i meridiani. Anche lo stesso miglio nautico è definito in base alla lunghezza media di un meridiano.
Creato il reticolo di riferimento, sono stati individuati gli "assi" di riferimento da cui misurare le distanze che rappresenteranno le coordinate geografiche: considerato che l'unico cerchio massimo dei paralleli è l'Equatore, questo sarà l'asse "orizzontale", quello che nel piano cartesiano era chiamato asse "X".
D'altra parte, essendo tutti i meridiani identici tra loro, per la definizione delle coordinate geografiche è stato necessario scegliere un meridiano di riferimento (il Meridiano di Greenwich) che rappresenta l'asse "verticale", quello che nel piano cartesiano era chiamato asse "Y".
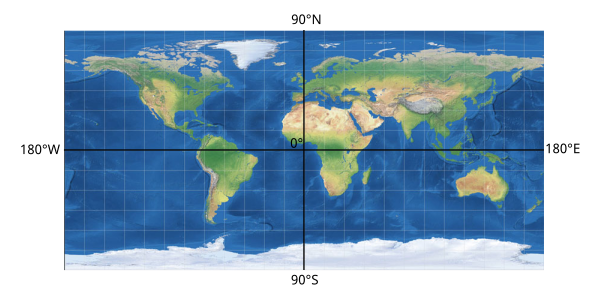
Riprendendo quello che si era detto per la "Longitudo" (la Longitudine) e la "Latitudo" (la Latitudine) e considerando che bisogna lavorare in un sistema sferico e non piano, nel sistema di coordinate geografiche sono stati mantenuti questi termini per indicare rispettivamente:
- Longitudine: misura la distanza angolare tra il Meridiano di Greenwich e il punto di cui voglio misurare le coordinate lungo i parelleli. Va da 0° (al meridiano di Greenwich) a 180° Ovest e da 0° a 180° Est. Spesso viene indicata con la lettera greca λ (lambda).
- Latitudine: misura la distanza angolare tra l'Equatore e il punto di cui voglio misurare le coordinate lungo i meridiani. Va da 0° (all'Equatore) fino a 90° Nord (al Polo Nord) e 90° Sud (al Polo Sud). Spesso viene indicata con la lettera greca φ (phi).
Questo sistema di coordinate geografiche (esattamente come nel piano cartesiano) permette di fornire la posizione assoluta attraverso la combinazione di Latitudine e Longitudine. Qui di seguito, ad esempio, sono riportate le coordinate geografiche di alcune città:
- Roma: Lat. 41°53.7'N Lon. 012°29'E
- New York: Lat. 40°43.1'N Lon. 073°59.9'W
- Tokyo: Lat. 35°40.7'N Lon. 139°45.5'E
Come si può notare, per convenzione i gradi della Longitudine si indicano sempre con tre cifre per differenziarla facilmente dalla Latitudine che ne può avere solo due (potendo andare da -90° a +90°).
Per maggiori informazioni su come convertire le i decimali di grado in primi di grado e viceversa, potete fare riferimento alla pagina delle formule utili per il carteggio nautico.
Cartografia e rappresentazione della Terra
Tuttavia, una cosa è indicare le coordinate su un piano e un'altra è riportare su un piano una geometria sferica come quella della Terra.
La cartografia è esattamente la scienza che si occupa di rappresentare la superficie terrestre su un piano. Poiché, per quanto vogliano dirne i terrapiattisti, la Terra è assimilabile a una sfera (più precisamente è un geoide), la sua rappresentazione su una superficie bidimensionale richiede un'operazione di proiezione e ogni proiezione comporta inevitabilmente delle distorsioni.
Ogni carta geografica è adatta a un certo tipo di utilizzo e per ogni utilizzo c'è una proiezione "preferita".
La Proiezione di Mercatore
La proiezione di Mercatore è quella preferita per le carte nautiche. Come tutte le proiezioni, introduce delle distorsioni (specialmente sulle aree).
Ma andiamo più nel dettaglio e vediamo quali sono le sue caratteristiche: sviluppata dal geografo fiammingo Gerardus Mercator nel XVI secolo, è una proiezione "cilindrica" e "conforme".
Il fatto che sia "cilindrica" ci dice che, a partire da un'origine di proiezione situata al centro della Terra, la superficie su cui si vanno a proiettare gli elementi geografici è un cilindro che circonda la Terra ed è tangente ad essa al livello dell'Equatore.
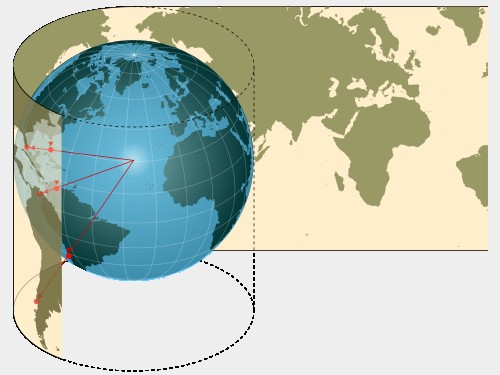
La caratteristica di "conformità" ci dice che la proiezione conserva gli angoli e le forme locali e, soprattutto, mantiene costanti gli angoli per le rotte di navigazione. Le rotte ad angolo costante, chiamate "lossodromie" (dal greco "percorso obliquo"), tagliano tutti i meridiani con lo stesso angolo e appaiono come linee rette sulla carta di Mercatore. Per questo motivo sono molto semplici da tracciare.
Altre caratteristiche notevoli della proiezione di Mercatore sono le seguenti:
- trasforma i meridiani in rette parallele verticali e i paralleli in rette orizzontali
- distorce le aree man mano che ci si avvicina ai poli e, per questo, si parla di proiezione a latitudini crescenti: i paralleli non hanno una distanza costante gli uni dagli altri ma la distanza tra loro aumenta andando verso i Poli.
- non è adatta a rappresentare le aree polari.
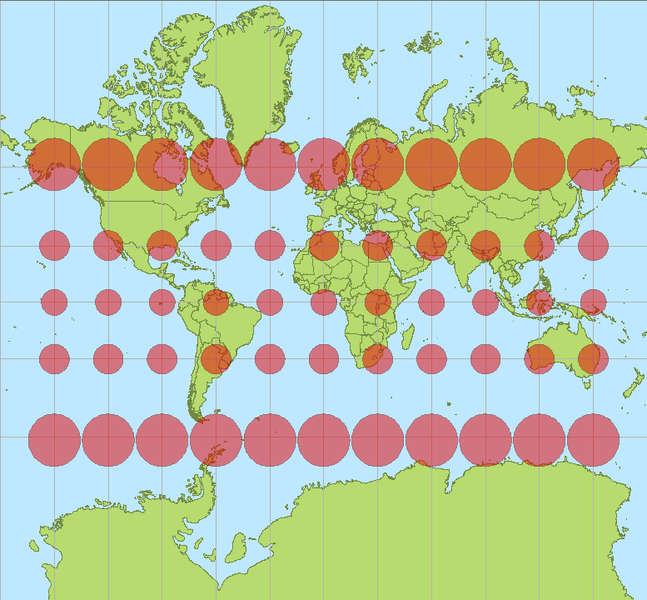
Credits: Stefan Kühn, CC BY-SA 3.0, via Wikimedia Commons
Lossodromie e ortodromie
È importante notare come per lunghe distanze le lossodromie non rappresentino il percorso più breve tra due punti. Questo succede perché sulla superficie della Terra (quindi in geometria sferica) il percorso più breve tra due punti e quello che segue il cerchio massimo che congiunge i due punti. Questo percorso si chiama "ortodromia" (dal greco "percorso dritto").
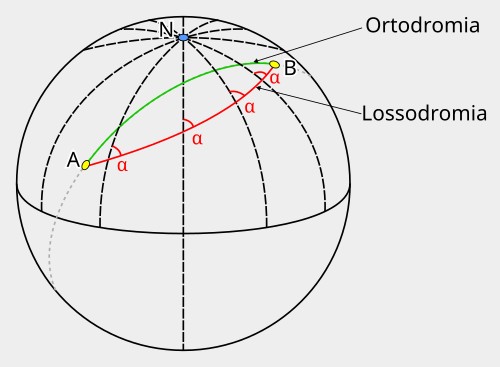
Come abbiamo detto prima, le lossodromie mantengono costante l'angolo con i meridiani (l'angolo α nell'immagine sopra) quindi, se si estendessero fino ai poli, formerebbero una spirale che andrebbe a terminare proprio nei poli.
Perché, quindi, per la navigazione si usano (quasi) sempre le carte di Mercatore anche se producono dei percorsi più lunghi in base alle lossodromie? Be', perché di solito gli spostamenti in barca sono abbastanza "locali" e per piccole distanze la differenza tra lossodromia e ortrodromia non è così accentuata.
Tuttavia, in caso di navigazione aerea o comunque per distanze molto lunghe, bisogna assolutamente tenere conto di questa differenza! E, infatti, nei voli intercontinentali gli aerei seguono rotte ortodromiche che sulla carta di Mercatore sembrano più lunghe ma che nella realtà sono le più brevi possibili per contenere al massimo i consumi di carburante.
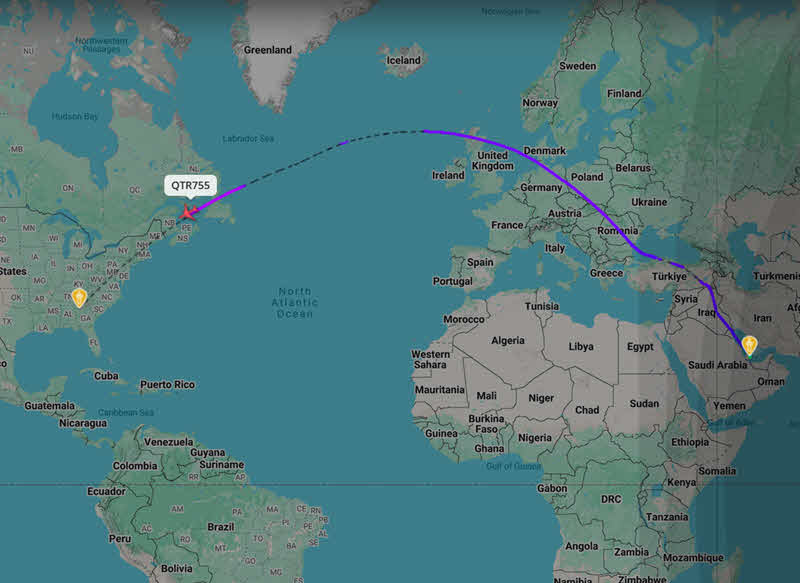
Le carte gnomoniche
Per tracciare correttamente i percorsi da seguire su grandi distanze è necessario utilizzare un altro tipo di carte, chiamate carte "gnomoniche".
Le carte gnomoniche utilizzano la proiezione gnomonica, appunto, che, a differenza di quella di Mercatore, non è conforme, cioè non mantiene gli angoli e le forme locali. Il pregio principale delle carta gnomoniche è quello di rendere possibile il tracciamento rettilineo delle ortodromie.
Infatti, se dovessimo tracciare il percorso più breve tra Lisbona (Portogallo) e Jacksonville (Florida), avremmo qualcosa del genere:
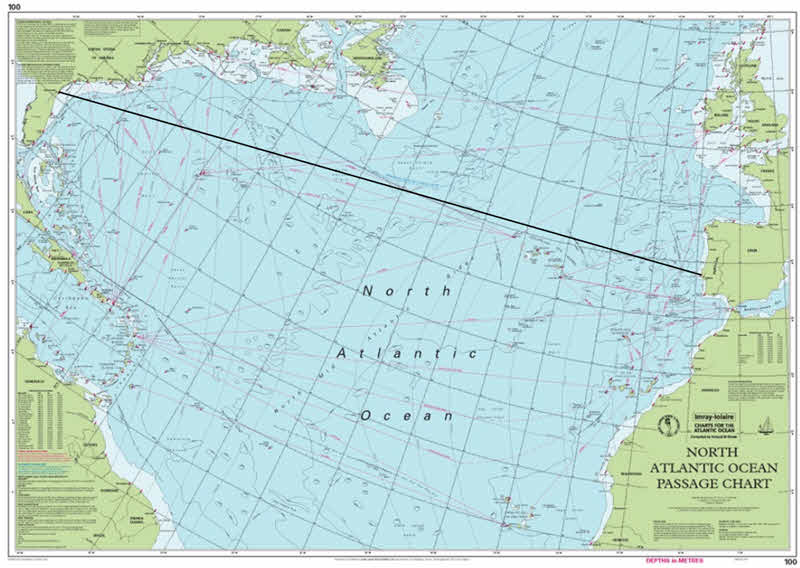
Possiamo ben vedere come l'ortodromia che abbiamo tracciato tagli i meridiani con angoli sempre diversi. Ciò significa che per percorrerla dovremo correggere la rotta ogni preciso numero di miglia, in base a quanto vogliamo stare più vicini ad essa.
Visualizzazione delle coordinate e dell'ortodromia
Nello strumento qui sotto (per cui si raccomanda l'utilizzo di un laptop) potrete divertirvi a muovere due punti sulla sfera terrestre e a vedere come cambiano le loro coordinate (Latitudine e Longitudine) e come cambia anche l'ortodromia che li congiunge. Inoltre, potete ruotare la Terra cliccando col mouse su di essa.

Classificazione delle carte nautiche
Le carte nautiche sono classificate in base alla scala. Andiamo a capire meglio cosa si intende per "scala" di una carta geografica: per poter rappresentare correttamente distanze ed estensioni anche molto grandi in modo da farcele stare in un foglio facilmente utilizzabile è necessario mantenere i rapporti tra tutti gli elementi rappresentati ma rimpicciolirli. In sostanza la scala è l'indicazione che ci dice qual è il rapporto di grandezza tra quanto è rappresentato e la realtà. Se siamo di fronte a una carta con scala 1:10.000 (uno a diecimila) sappiamo che 1 centimetro sulla carta equivale a 10.000 centimetri nella realtà, cioè 100 metri.
È quindi chiaro come per rappresentare porzioni di territorio o mare più o meno grandi è necessario avvalersi di carte geografiche a scala diversa in base al tipo di informazione che ci serve conoscere. Avremo quindi:
- Carte generali, con scala di 1:3.000.000 o inferiore, utili per la navigazione a lunga distanza
- Carte costiere, con scala di 1:100.000, utili per la navigazione costiera
- Piani o "pianetti" nautici, con scala di 1:5.000, utili soprattutto per rappresentare i porti o gli approdi.
Quando si parla di "piccola scala" o "grande scala" non bisogna farsi confondere al numero piccolo o grande che troviamo subito dopo l'"1:". Infatti, poiché la scala rappresenta un rapporto (quindi una divisione), più il denominatore (cioè il numero che segue l'"1:") è grande, più sarà piccolo il rapporto e quindi più piccola sarà la scala.
Facciamo un esempio con numeri semplici:
- 1:20
- 1:100
- 1:5
- 0.05
- 0.01
- 0.2